Введение

В настоящее время геополитические процессы, протекающие на мировой арене настолько многообразны и непредсказуемы, что любой прогноз становится маловероятным, с точки зрения его реализации.  Но в целом, можно отметить основную тенденцию, которая характеризует современную политическую обстановку в мире, а именно, за последние годы значительно возросла агрессивность США и их сателлитов в отношении России. Причем свою агрессивность «коллективный разум» Запада оправдывает ничем неподкрепленными фактами и абсолютно немотивированной ложью. В эти тенденции укладывается и противодействие Северному потоку-2, высылка дипломатов, наложение санкций, развертывание вооруженных сил НАТО на границах России и т.д.  С точки зрения возможности дать адекватный ответ на внешние вызовы, вплоть до военных, огромное значение имеет силовая составляющая государства и, в частности Вооруженные Силы РФ. Основная сдерживающая сила, которая не позволяет холодной войне с Западом перейти в горячую фазу это ядерная триада ВС России, где важнейшее место принадлежит атомным подводным лодкам стратегического назначения.  Но без радиоэлектронного обеспечения и, в частности, гидроакустических средств, подводная лодка становится «слепой» и «глухой» и неспособна выполнять задачи по своему предназначению. В связи с этим тематика настоящей статьи, направленная на формирование сложных широкополосных сигналов, обладающих высокой разрешающей способностью по параметрам и скрытностью, является актуальной и обладает не только с теоретической, но и практической значимостью.

Сложные сигналы и факторы, ограничивающие их применение в гидроакустике

Анализ классов гидроакустических сигналов показал, что одним из перспективных направлений является использование сложных широкополосных сигналов (СШС). Это обусловлено тем, что сложные сигналы, к примеру, основанные на кодировании и фазовой манипуляции, показавшие высокую эффективность в радиолокации, в силу особенностей гидроакустического канала не всегда оказываются столь же эффективными в гидроакустике, так как инерционность среды приводит при перебросе фазы к паразитной амплитудной модуляции, что сводит на нет все преимущества кодовой манипуляции. В настоящее время применение кодовой манипуляции в гидроакустики ограничивается огибающей сигнала. На несущей частоте более перспективными представляется класс частотно-модулированных сигналов. Но эти сигналы имеют достаточно высокий уровень боковых лепестков и недостаточно адаптированы к методам цифровой обработки. При этом псевдослучайные сигналы просто формируются и обрабатываются, так как основаны на использовании линий задержки и КИХ-фильтрах, поэтому легко реализуются цифровыми средствами.

В целом необходимо отметить, что в настоящее время все методы синтеза сигнала в основном ориентируются на временной подход. В частности, синтез частотно-модулированных сигналов (ЧМС) основан на задании функции модуляции во временном представлении. Спектральное представление является лишь следствием этого подхода. При этом оптимальные системы обработки ЧМС достаточно сложны в реализации.

В принципе, можно сказать, что все сигналы по топологическому признаку (без учета дискретизации и квантования) в области частот можно разделить на четыре класса:

1. Многочастотные (полигармонические).
2. Многополосные (полосовые).
3. Непрерывные.
4. Комбинированные.

В случае излучения компонент МЧС одновременно временное представление носит характер отличный от случая, когда компоненты излучаются последовательно, но энергетический спектр носит аналогичный характер. Отличие заключается лишь в полосе спектральной компоненты, что объясняется тем что общая длительность компонент сигнала больше чем при последовательном излучении.  Во временной области вид сигналов существенно отличаются друг от друга.

Если энергетические спектры сигналов подобны, то можно сделать вывод, что различие временных представлений определяется только фазовым спектром. Из примера следует, что спектральное представление имеет «две степени свободы» в отличии от временного, поэтому энергетический спектр (ЭС) можно выбрать заранее, а учитывая, что преобразование Фурье от ЭС определяет автокорреляционную функцию (АКФ) зондирующего сигнала, его можно выбрать из класса спектров соответствующих хорошим АКФ. Но задание одного ЭС недостаточно, так как в среде распространяется сигнал, определяемый пространственно-временным представлением.

Известно, что гидроакустика и радиолокация двигаются в определенной степени параллельно. Но целый ряд факторов не позволяет воспользоваться в гидроакустике, теми возможностями, которыми уже давно пользуется радиолокация. К таким факторам ограничениям можно отнести: частотно-зависимое затухание гидроакустического сигнала, флуктуации океанической среды, многолучевость распространения, низкое значение интервала когерентности по времени (от 200÷500 длин волн), высокое значение числа Маха, что затрудняет использование классической функции неопределенности (ФН).  

Из вышесказанного следует, чтобы решить проблему синтеза гидроакустических сигналов необходимо ее решать в жестких условиях вышеперечисленных ограничений.  В данной статье предлагается подход, основанный на принципе дуальности, который позволяет в определенной степени снять эту проблему.

Принцип дуальности и синтез сигналов

Известно, что любой сигнал может быть представлен во временной и спектральной области. Причем спектральное представление неоднозначно, в том смысле, что определятся выбором базисных функций.   Критерием оптимального спектрального представления является системный принцип минимального описания, сущность которого сводится следующему: описание оптимально, если без потери информации оно требует наименьшее число базисных функций. Тот или иной набор базисных функций диктуется типом симметрии сигнала. Формулы, описывающие комплексные огибающие, спектры и корреляционные функции частотных и дискретных сигналов для различных групп и цепочек преобразований рассматривались в работах [4-8].

Частотно-временная дуальность частотных и дискретных сигналов. Дуальность сигналов приводит к дуальности частотных и дискретных сигналов. В частности, из сравнения формул для этих сигналов видно, что структурно они имеют одну и туже форму, но временные зависимости заменяются частотными, а частотные зависимости – временными. Точно такой же вывод следует из сравнения спектра комплексной огибающей частотного сигнала с комплексной огибающей дискретного сигнала. Из частотно-временной дуальности частотных и дискретных сигналов следует, что эти сигналы должны обладать одинаковыми свойствами «с точностью до поворота частотно-временной плоскости на». Поэтому, если определено, то или иное свойство для одних сигналов, оно может быть перенесено на другие сигналы с заменых частотных зависимостей на временные и наоборот [1-3]. 

Таким образом, основой подхода к формированию сигналов, который открывает определенное направление в области теории и применения гидроакустических сигналов, является принцип дуальности. В соответствии с этим принципом, синтез сигналов предлагается проводить в спектральной области [5,6]. Рассмотрим этот подход поэтапно.

1. Исходя из решаемой задачи определяется частотный диапазон, который будет занимать зондирующий сигнал. Этот выбор должен учитывать влияние доплеровского эффекта и частотный диапазон антенны.  
2. Спектральный метод синтеза предполагает задание энергетического спектра сигнала и его фазового спектра. На выбор ЭС влияют такие требования как:

• пик-фактор не должен быть большим;
• корреляционная функция не должна иметь больших боковых лепестков и добавочных максимумов.

Базовой теоремой на основании которой синтезируется гидроакустический сигнал является теорема Винера-Хинчина в соответствии с которой энергетический спектр и автокорреляционная функция сигнала связаны парой преобразования Фурье:

 .

Как будет показано ниже, в класс энергетических спектров, которые могут быть использованы в качестве базовых [6], входят:

• полигармонические сигналы, компонентами которых являются разно частотные гармоники. Причем их формирование возможно при условии:

• число  степеней  свободы сигнала  ;
• длительности компонент полигармонического сигнала одинаковы ;

• комбинированный метод, включающий первых два условия.

• Полосовые сигналы, компонентами которых являются сложные узкополосные сигналы, расстановка центральных частот которых, удовлетворяют условиям обозначенных выше.
• Сигналы с непрерывным спектром.

Важно отметить, что расстановка ПГС и ПС по оси частот может проводиться чрез равные интервалы, по какому-либо закону и случайным образом. Главное условие, чтобы компоненты ПС не пересекались, т.е. скалярное произведение компонент было равно нулю.

3. Выбор фазового спектра. Задание энергетического спектра недостаточно, чтобы сформировать зондирующий сигнал. Излучаемый сигнал является действительным его спектр является комплексным, поэтому необходимо задать фазовый спектр. Условия выбора сводится к следующему: начальные фазы для каждой компоненты полигармонического сигналы были различными. В противном случае суммарный сигнал во времени будет представлять собой сигнал с большим всплеском в начале. В этом случае, о никакой скрытности говорить не приходится. Фазовый спектр может быть задан как детерминированная функция частоты или как некоторый случайный процесс.
4. Формирование комплексного спектра:   .
5. Вычисление временного представления ШПС:  
6. Проверка сигнала на пик-фактор и в случае необходимости принять меры по его снижению.

Спектральный синтез сигналов позволяет создать сигналы достаточно сложной структуры, так появляется возможность кодировать сигналы не только во времени, но и по частоте. В спектре, в отличие от временного представления сигнала, есть две степени свободы: энергетический и фазовый спектр, вид которых можно варьировать независимо друг от друга. Таким образом, предлагаемый подход к формированию зондирующего сигнала позволяет «размазать» энергию сигнала на плоскости время и частота. Рассмотрим пример. Предположим, что верхняя частота спектра равна 15 000 Гц. Тогда длительность сигнала, соответствующая этой частоте равна 0.1 мс.  Если положить, что число степеней свободы сигнала равно 1000, то пространственный размер сигнала равен 100. Откуда получаем максимальную длительность, соответствующую заданной частоте мс. Предположим, сигнал широкополосный и полоса равна 10 000 Гц.  Тогда максимальная база  , которая может быть получена при заданных условиях 140. Если число волн не превышает 1000, то при  заданной полосе (коэффициент узкополосности )  большую базу сигнала получить не возможно. Но база сигнала привязана к частоте, поэтому в гидроакустике есть смысл использовать обработку на несущей частоте.,  ().

Пик-фактор многочастотных сигналов

Гидроакустический сигнал во временной области должен обладать достаточно низким пик-фактором, чтобы обеспечить равномерное распределение мощности сигнала в пределах его длительности. Пик-фактором «Π» сигнала будем называть отношение наибольшей (пиковой) мощности к средней мощности сигнала на длительности символа:

        .              

Тогда пик-фактор многочастотного сигнала определяется следующим выражением:

           .                

Если спектральные компоненты равны по амплитуде, т.е. , то получим:  и пик-фактор многочастотного сигнала определяется следующим выражением:

    .                     

Методы снижения пик-фактора могут быть классифицированы как не искажающие и искажающие. Не искажающие методы уменьшают пик-фактор без введения нелинейных искажений. В искажающих методах нет необходимости в передачи дополнительной информации, тем не менее, эти методы являются более вычислительно сложными и могут также приводить к снижению скорости передачи, как правило, из-за расширения спектра и/или ухудшения помехоустойчивости.  Минимальный пик-фактор равный единице имеют сигналы типа меандра. Но такие сигналы в гидроакустической среде не распространяются, они сглаживаются уже в системе генерации и излучения сигнала. Для сигнала типа меандра спектр имеет бесконечную ширину, но он физически ограничивается системой генерации в антенне. В акустической среде распространяются сигналы типа гармонических, а также сигналы, которые можно представить, как совокупность гармоник. Для гармоники пик-фактор  равен .  Псевдослучайные последовательности, которые получают манипулированием фазы гармонического сигнала имеют пик-фактор 1, но только для его огибающей. Шумоподобный сигнал имеет пик фактор до 3. Как будет показано ниже существуют различные способы понизить пик-фактор, которые практически не влияют на корреляционную функцию и ФН.

Методы синтеза сигналов

В данном пункте будут рассмотрены основные методы синтеза сигналов, которые ориентированы на синтез сигналов со свойствами, вытекающими из основных свойств ФН, которые характеризуют основные свойства сигнала: разрешающие способности и точности по тем или иным параметрам.

Известно, что каждому сигналу соответствует функция неопределенности, которая рассматривалась как его внутренняя характеристика. В целом, эта классическая ФН адекватно описывает, только преобразования узкополосных сигналов.  В частности, ФН Вудворда описывает симметрию сигнала относительно сдвиговых преобразований в области времени и частоты при наличии эффекта Доплера. Но для широкополосных сигналов эффект Доплера приводит к преобразованию сжатия (растяжения) сигнала и во временной и в спектральной области и поэтому требуется обобщение ФН [4,6.7].   

Широкополосная функция неопределенности (ШФН) определяется следующим выражением [4,7]:

.                                                (1)

Все многообразие свойства ШФН подробно рассмотрены в работах [4,7]. Но для задачи синтеза сигналов определяющими являются следующие:

1. При нормированной плотности функция неопределенности для широкополосного сигнала имеет максимальное значение равное единице: 

.

2. Объем «тела неопределенности» в случае широкополосного сигнала, зависит от формы сигнала:

.

Объем тела неопределенности равен единице только в случае если определять энергию по двум мерам аддитивной м мультипликативной .  Другой вариант определять широкополосную ФН с весовым окном:

  [7]:

,               (2)

.

Функция неопределенности определяет свойства сигнала и является его внутренним свойством. Роль этой функции сводится к тому, что по ней можно сравнивать различные виды и формы сигналов с точки зрения точности и разрешающей способности по дальности и скорости. Естественно, возникает общая проблема синтеза сигналов по ФН, т. е. задача определения сигнала s(t), реализующего желаемую ФН. Эта весьма сложная проблема, по существу, включает в себя ряд частных взаимосвязанных задач, каждая из которых имеет самостоятельное практическое значение.

Здесь можно указать, например, следующий круг вопросов:

а) определение класса функций, реализуемых как ФН при произвольных сигналах;

б) определение подклассов ФН, точно реализуемых при помощи сигналов той или иной конкретной структуры (ЧМ импульсов, фазоманипулированных кодовых групп и т. д.), а также отыскание сигналов, создающих эти ФН;

в) расчет сигналов, ФН которых достаточно хорошо аппроксимируют (в том или ином смысле) желаемые функции, не принадлежащие к классу реализуемых;

г) изучение оптимальных для выбранного подкласса функций ФН и соответствующих им оптимальных сигналов, наилучшим образом удовлетворяющих некоторой совокупности частных требований (например, синтез ЧМ сигналов, обеспечивающих наилучшее разрешение по дальности при отсутствии требований по частотному разрешению).

Надо сказать, что задача синтеза сигналов, ФН которых обладают желаемыми свойствами, в настоящее время до конца не решена. Для узкополосных сигналов можно определить необходимые и достаточные условия определения сигнала по реализуемой ФН. Но как показано в работе [1] теоретическое решение на практике почти ничего не дает по следующим причинам:

1. Это решение пригодно только для реализуемых функций неопределенности, а, как правило, нужно искать приближения к произвольным функциям и случаи реализуемости весьма редки.
2. Для решения необходимо знать не только модуль, но и фазу ФН, в то время как из практических соображений можно задать только желаемый закон изменения модуля и неизвестно, какой фазовой функции этот модуль соответствует.
3. Приступая к синтезу, приходится задаваться фазой, что приводит к неоптимальным решениям. Для проверки качества приближения нужно произвести расчеты для различных фазовых функций и оценить погрешность в каждом случае.  Разумеется, такие расчеты весьма сложны, а эффективность их заранее неизвестна.

Таким образом, точное решение не удается получить даже в тех случаях, когда модуль выбранной функции неопределенности реализуем. Синтез широкополосных сигналов по функции неопределенности, становится еще более проблематичным. Это связано прежде всего с тем, что объем тела неопределенности ШФН не является постоянным.

В работах [1-3] рассматривался синтез сигналов по корреляционной функции. Эти методы направлены в основном, на формирование корреляционной функции в области главного максимума. Но как показывает анализ, такой подход не всегда оказывается конструктивным, так как первичным все-таки является полоса пропускания фильтра, к которому можно отнести: антенну, сигналы на входе системы временной обработки сигналов и т.д. Таким образом при синтезе сигналов надо ориентироваться на спектр сигнала (энергетический и фазовый спектр). Полоса частот пропускания является физическим фактором, который определяется фундаментальными законами природы. Корреляционная функция есть результат преобразования Фурье над спектральной плотностью, но она вторична и поэтому как бы не привлекательно было бы синтезировать сигнал по корреляционной функции, все равно привязку к реалиям мы вынуждены делать исходя из полосы пропускания.  

Синтез сигнала в спектральной области

Синтез зондирующего гидроакустического сигнала в спектральной области с заданными характеристиками можно представить в виде схемы представленной на рис.1. В соответствии с рис.1 исходя из поставленных задач формируется кортеж параметров энергетического спектра (ЭС) и фазового спектра (ФС): 

.               (3)

Где      – верхняя и нижняя частота ЭС и ФС, ширина спектра;  

   –  i-ая ширина спектра компоненты сигнала и частотный сдвиг между компонентами соответственно;

,  –  амплитуда ЭС и временная длительность сигнала.

Необходимо сказать, что при формировании энергетического и фазового спектров зондирующего сигнала необходимо учитывать свойства среды: вертикальное распределение скорости звука по глубине, интервалы когерентности по времени и частоте, частотно-зависимое затухание, флуктуации среды, законы распределений помех и шумов и т.д.  В блоке формирования энергетического спектра, в зависимости от решаемых задач, выбирается один из классов ЭС: ПГС, ПС или непрерывный. 

Следует отметить, что этими тремя классами и их комбинацией можно описать все многообразие ЭС, так как дальнейшая детализация определяется кортежем параметров (3).  При выборе ПГС и ПС требуется знать параметры расстановки компонент . Закон расстановки компонент: может случайным, детерминированным или смешанным.  В частности, при детерминированном законе возможны варианты равномерной расстановки, по какому-нибудь закону: линейному, квадратичному и т.д., или расставлять как псевдослучайную последовательность, используя различные кодовые комбинации (коды Баркера, М-последовательность, многочастотные сигналы и т.д.).  При стохастической расстановке можно использовать генераторы случайных чисел в заданном диапазоне частот. Значения каждой случайной величины будет соответствовать центральной частоте ПС или ПГС.  После выбора ЭС необходимо проверить какой уровень боковых лепестков (БЛ) и наличие добавочных максимумов (ДМ) в автокорреляционной функции (АКФ).  В случае, если после проверки АКФ уровень БЛ достаточно большой, можно воспользоваться сверткой АКФ с выбранной весовой функцией .  Весовая функция позволяет значительно уменьшить БЛ, но это достигается некоторым расширением главного максимума АКФ. 

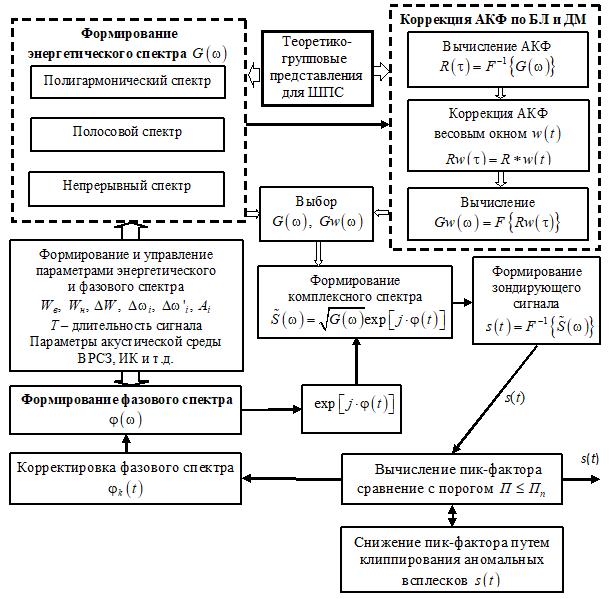
Рисунок1 – Структура формирования зондирующего сигнала

После этого с помощью преобразования Фурье вычисляется скорректированный энергетический спектр. Далее принимается решение какой ЭС использовать при формировании комплексного сигнала.  Сформированный комплексный спектр подвергается преобразованию Фурье и далее временной сигнал подается в устройство определения пик-фактора. В случае если пик-фактор превышает пороговое значение , то принимается решение о снижении пик-фактора или ограничением аномальных всплесков во временном представлении сигнала или корректировкой фазового спектра. После корректировки в  случае если  сигнал полагается сформированным и готовым к применению для решения тех или иных задач. Путь ограничения по аномальным всплескам, как показал модельный эксперимент является очень эффективным способом понижения пик-фактора и почти не искажает сигнал , но в принципе, он является нелинейным.  Другой подход основан на корректировке фазового спектра. Но такой подход является эвристическим, поэтому подбор фазового спектра можно осуществлять пока, в основном, путем проб и ошибок. Этот вопрос требует дальнейших исследований. 

Необходимо отметить, что для широкополосных сигналов необходимо учитывать преобразования, связанные с кинематикой источника и приемника гидроакустических сигналов. Эти преобразования приводят к теоретико-групповым представлениям сигналов и определения собственных функций этих преобразований, являющихся аналогами гармоникам Фурье и изоморфные им. В частности, при линейном преобразовании имеет место два преобразования: аддитивное и мультипликативное (сдвига и сжатия).

Таким образом, пользуясь принципом дуальности можно ввести «альтернативную теорию» сигналов где, к примеру, возможно построить М-последовательность в спектральной области. При этом появляется дополнительная возможность независимо варьировать, для обеспечения необходимых свойств сигнала, фазовым спектром. Кроме этого повышается скрытность сигнала [6].

Как известно, амплитуда отраженного от цели сигнала зависит от целого ряда факторов, в том числе, и от эффективной площади рассеяния объекта. Для соотношений между используемыми в радиолокации (аналогично и в гидроакустике) длинами волн и размерами типовых целей эффективная площадь рассеяния цели является достаточно сильно осциллирующей величиной. Такой эффект вызывает сильную флюктуацию амплитуды отраженного сигнала, что приводит к уменьшению требуемого отношения «сигнал-помеха» (ОСП), а это отрицательно сказывается на характеристиках радиолокатора, таких, как дальность обнаружения цели и точность измерения ее координат.

Отрицательное влияние флюктуации отраженных сигналов на характеристики гидроакустических средств может быть устранено или, по крайней мере, уменьшено, если удастся каким-либо образом добиться их сглаживания. Одним из способов сглаживания флюктуации является применение многочастотных сигналов. Физическая сущность эффекта сглаживания флюктуации отраженного сигнала при облучении цели многочастотным сигналом состоит в том, что при достаточно большом разносе несущих частот ширина лепестков диаграмм вторичного излучения цели на различных частотах неодинакова, а соответствующие экстремальные точки диаграмм оказываются сдвинутыми друг относительно друга, благодаря чему уменьшается изрезанность эквивалентной диаграммы вторичного излучения цели и соответственно относительная величина флюктуации отраженного сигнала. При этом наибольший эффект сглаживания флюктуации достигается при статистической независимости отраженных от цели сигналов на каждой из составляющих частот [1-3].

Главное достоинство многочастотных сигналов:

• высокая помехозащищенность, что обусловлено, прежде всего, высокой помехоустойчивостью самого метода многочастотной гидролокации;
• применение специальных способов совместной обработки сигналов с разными несущими частотами;
• возможностями перераспределения излучаемой энергии между различными частотными каналами;
• выигрыш в пороговом отношении сигнал/шум. 

Как было отмечено выше многочастотный сигнал (МЧС) — совокупность одновременно передаваемых сигналов с различными несущими частотами и законами модуляции. Первоначально применялся в радиолокации с целью повышения надёжности его обнаружения путём сглаживания флуктуаций отражённого от цели сигнала. Кроме этого, многочастотные сигналы применяются в системах мобильной связи четвёртого поколения. Преимуществом использования многочастотных сигналов для передачи информации является высокая устойчивость к помехам. При этом вероятность одновременного пропадания отраженного сигнала с несколькими несущими частотами меньше, чем одночастотного сигнала. Многочастотные сигналы, в простейшем случае двухчастотный сигнал, так же оказываются эффективным средством борьбы со «слепыми скоростями». При этом в такой двухчастотной когерентно-импульсной системе число слепых скоростей в диапазоне рабочих скоростей значительно меньше, чем в соответствующей ей одночастотной PJIC [9]. Кроме того, проведено сравнение двухчастотной системы и системы со сменными периодами повторения импульсов. Показано, что первая система обработки при медленных флюктуациях обладает заметными преимуществами по сравнению со второй, что является следствием относительного уменьшения флюктуаций цели при многочастотном зондировании.

При многочастотном сигнале уже недостаточно рассматривать функции автокорреляции каждой из его частотных составляющих, а необходимо ввести также функцию их взаимной корреляции. При практическом использовании многочастотного сигнала стремятся обеспечить независимость отраженных от щели сигналов на каждой из составляющих частот, что позволяет производить независимую их обработку (умножение каждого из сигналов на ожидаемый сигнал и интегрирование). Необходимым, но не достаточным условием независимости отраженных сигналов является ортогональность соответствующих составляющих зондирующего сигнала. Достаточность достигается лишь при не перекрывании спектров компонент, т. е. при достаточно большой величине разности частот. В дальнейшем в случае многочастотного сигнала это условие будем считать выполненным.

Функция неопределенности широкополосного сигнала

Как было показано выше свойства гидроакустических (радиолокационных) сигналов, которые характеризуют особенности измерения дальности и скорости целей, описываются функцией неопределенности Вудворда. В частности, известное ограничение частотной разрешающей способности при спектральном анализе, связанное с конечным временем наблюдения, можно трактовать как разновидность соотношения неопределенностей. В данном пункте будут рассмотрены ШФН многочастотных (полигармонических и полосовых) сигналов. Широкополосная ФН сигналов с непрерывным спектром представлена выражениями (1) и (2) а ее обобщения на произвольные группы преобразований рассмотрены [4,7,8]. 

Для широкополосных сигналов ФН требует обобщения, так как частотный сдвиг по частоте не является адекватной математической моделью эффекта Доплера. Излученный мономногочастотный сигнал (ММЧ-сигнал) представляет собой сумму  гармонических частотных компонент , модулированных по амплитуде общей огибающей импульса , который может быть задан выражением:

                              .                                       (4)

Многочастотный сигнал может быть реализован или последовательным излучением импульсов с разной частотой заполнения (скважность больше или равна нулю) или одновременным излучением всех частотных компонент.

В общем случае частоты компонент многочастотного сигнала произвольны. Рассмотрим простейший случай равномерного распределения частот с постоянным шагом . Тогда текущая частота может быть представлена в следующем виде:

,   ,   .              

Другие варианты распределения частот: случайное, в виде кодовых последовательней, функциональных зависимостей. Все эти зависимости влияют на форму функции неопределенности в области боковых лепестков в координатной плоскости «задержка-скорость». Форма огибающей  может быть различной, однако ее эквивалентная длительность  связана с шагом по частоте соотношением вида:

                                     ,    .                                             (5)

В этом случае разрешающая способность по дальности может быть определена по формуле:

                           ,  .                                       

При этом мы получаем разрешающую способность в раз более высокую, чем размер импульсного объема . При этом частотный шаг  при равномерной сетке частот определяет интервал однозначной дальности измерения , точно равный импульсному объему . Из равенства вытекает свойство ортогональности компонент ММЧ-сигналов (области определения каждой компоненты ММЧ - сигнала не пересекаются). Действительно, при прямоугольной огибающей единичной амплитуды и длительности  с учетом формулы (5) имеем:

            .                     (6)

                                          .                                                       

При   и всех значениях целого числа  значение в правой части выражения (6) равно нулю, а при  это значение равно , так как .  Используя символ Кронекера  , можно записать

                        при                                     

При нецелых значениях  ортогональность компонент прямоугольного ММЧ-импульса нарушается (их частотные полосы перекрываются).

Другим вариантом ортогональных компонент ММЧ сигнала являются компоненты с прямоугольным спектром с шириной полосы , меньшей, равной или большей частотного шага , они будут рассмотрены ниже. Необходимо отметить, что реальные сигналы с прямоугольной огибающей, как и с прямоугольным спектром, физически нереализуемы, так на границах прямоугольника производная по времени (частоте) принимает значение равное бесконечности. Так как производная есть скорость изменения состояния, а в природе нет бесконечно больших скоростей, то любые скачкообразные изменения состояния физически нереализуемы. Поэтому и условие ортогональности компонент зондирующего МMЧ сигнала выполняется лишь приближенно. Чем дальше будут друг от друга компоненты МMЧ сигнала, тем лучше будет выполняться условие ортогональности. В этом смысле компоненты реальных ММЧ сигналов, близкие по форме огибающей или спектра к прямоугольным, при указанных выше условиях ортогональности можно считать лишь квазиортогональными, т. е. значение интеграла вида (6) при  существенно меньше его значений при , равных энергии соответствующей компоненты. В строгом смысле перестают быть ортогональными компоненты на частоте  зондирующего (опорного) МMЧ – сигнала и компоненты на частоте  задержанного на произвольное время  принимаемого (отраженного от цели) сигнала [9].

Функция неопределенности полигармонического сигнала. Приведенные соображения учитываются при вычислении корреляционных интегралов согласованной обработки ММЧ – сигналов. Модуль корреляционного интеграла для точечной частотно независимой цели совпадает с точностью до нормировки с ФН ММЧ-сигнала по задержке и скорости цели. При заданной радиальной скорости цели  и СШП МЧ – сигнале каждая его частотная компонента  вследствие большой разности даже соседних парциальных частот  и  приобретает свой доплеровский сдвиг частоты [9]: 

                               ,   ,                                           

где    − скорость звука;  ;

 − параметр, пропорциональный радиальной скорости цели v и равный  

         частоте Доплера для  начальной компоненты, .

Если зондирующий сигнал задается выражением  вида (2) принимаемый сигнал с задержкой  и частотами Доплера ,  соответствующими радиальной скорости цели  можно представить как: .

                 .                             

− множитель распространения и отражения сигнала от цели на .

Опорный сигнал, согласованный с задержкой   и частотами Доплера  соответствующими скорости , можно представить аналогичным выражением:

              .                          

Интеграл от произведения сигналов и , определяет их корреляционное сравнение:

                 (7)

В принципе, ФН это внутреннее свойства сигнала, которое определяет его свойства относительно сдвига по времени и частоте. Физический смысл ФН можно придать если положить, сравнивается опорный сигнал и его отражение от некоторой подвижной цели находящейся на некотором расстоянии от локатора. При вычислении ФН обычно предполагаются частотно – независимый характер отражения от точечной цели и компенсация зависимости множителей распространения от частот  сигнальных компонент. Это позволяет при вычислении ФН считать множители  и  одинаковыми и равными единице, т. е.  Вычислим при этих предположениях корреляционный интеграл и функцию неопределенности ММЧ-сигнала (5) при прямоугольной огибающей импульса МЧ-сигнала длительностью :

С учетом конечной длительности и степени перекрытия прямоугольных импульсов  и , зависящей от , интеграл в выражении (5) сводят к интегралу в конечных пределах. При этом

• нижний предел
• верхний предел  зависят от .

Значение интеграла не равно нулю при и равно нулю при . Результат вычисления ФН, совпадающий с корреляционным интегралом (6) с точностью до множителя нормировки, имеет следующий вид:

        (8)     

где  − функция Хевисайда единичного скачка, которая определяется выражением:            

При некоторых условиях выражение (8) можно значительно упростить и представить в виде однократной суммы. В частности, при  значимыми в двойной сумме остаются лишь диагональные слагаемые при . Тогда получим:                        

     (9)

При дополнительном условии малых  можно, допустив и
дальнейшие упрощения в выражении (9), получить (имеют место соотношения ):

    .                 (10)  

При указанных дополнительных условиях справедливы следующие приближенные равенства: .    

Сечения (10) можно записать в аналитической форме как на основе точного выражения (8), так и на основе приближенной формулы (9):

             .                    (11)

При увеличении длительности прямоугольной огибающей спектр приобретает вид совокупности все более узких спектральных компонент. В противоположность этому с уменьшением длительности ММЧ-импульса происходит слияние отдельных спектральных компонент, и глубокие провалы в спектре исчезают. Простое физическое объяснение значительного улучшения разрешающей способности по скорости заключается в том, что частотные компоненты СШП ММЧ-сигнала могут весьма значительно отличаться по частоте друг от друга.

Столь же значительно отличаются и парциальные доплеровские сдвиги на этих частотах, чего не наблюдается в случае узкополосного сигнала, и доплеровские частоты в принятых и опорных, одноименных по частоте компонентах не совпадают. Именно это обстоятельство, характерное для СШП ММЧ – сигнала, приводит к дополнительному и существенному сужению главного лепестка сечения ФН по скорости в отличие от узкополосных многочастотных сигналов, частотные компоненты которых сдвигаются по частоте Доплера практически на одинаковую величину. Увеличение числа частот приводит
к некоторому снижению уровня «крыльев» сечения ФН вне пределов основного лепестка.

Функция неопределенности полосового сигнала. Рассмотрим ММЧ  сигнал с прямоугольным спектром каждой спектральной компоненты. Предположим, что ширина спектра каждой спектральной компоненты одинакова и равна . Представим огибающую  через спектр Фурье  [9]:

.                                 (12)

В случае прямоугольного спектра с полосой :

При этом огибающая импульса  имеет вид функции , т. е. обладает бесконечной длительностью и является физически нереализуемой, впрочем, как и прямоугольная огибающая импульса. Вместе с тем такие идеализации являются полезным приближением к реальным огибающим и существенно упрощают анализ, позволяя вычислить входящие в выражение для ФН интегралы свертки в конечной форме. После преобразования интеграла в выражении (12) с помощью теоремы о свертке [1-3,8] и свойств преобразования Фурье можно получить корреляционный интеграл в форме, выраженной через спектр огибающей :

.       (13)

Поскольку ФН совпадает с корреляционным интегралом (13) с точностью до множителя нормировки, то после подстановки выражения (13) в формулу (8) и вычисления входящего в эту формулу интеграла для ФН получим     

              (14)

,   .

При условии, что расстройка по частоте парциальных сигналов превышает ширину прямоугольного спектра огибающей  на величину, необходимую для отсутствия перекрытия спектров разных частотных компонент при передаче и приеме с учетом сдвига на частоту Доплера, будет обеспечена полная взаимная ортогональность частотных компонент опорного и принимаемого сигналов. В этом случае выражение (14) сводится к однократной сумме

      (15)

                       .                                   

Одномерные сечения по задержке и по скорости имеют вид:

.                     

Для прямоугольных спектров, так же как и для прямоугольного импульса ММЧ-сигнала, правые части равенств (14) и (15) практически не зависят от переменной .

Если спектр сигнала представляет собой совокупность прямоугольных компонент, близко расположенных друг к другу (спектр по сути дела является сплошным), то модуль корреляционного интеграла и сечение ФН по задержке не имеют дифракционных максимумов, и неоднозначность измерений по дальности отсутствует, как и для ММЧ импульса с прямоугольной огибающей. В случае ММЧ импульса с прямоугольной огибающей на краях однозначного интервала имеются недостаточно подавленные остатки дифракционных лепестков, полностью отсутствующие в ММЧ сигнале с прямоугольными спектральными частотными компонентами, не имеющими провалов в суммарном спектре излучения.

Характерно, что при , в отличие от случая, когда , уровни основного лепестка и остатков дифракционных максимумов находятся выше максимального уровня огибающей импульса соответствующего прямоугольного спектра, что свидетельствует о необходимости корректировки множителя нормировки ФН. Для обеспечения приемлемой разрешающей способности по скорости  следует выбирать ширину  полосы прямоугольной спектральной компоненты ММЧ сигнала, исходя из эффективной длительности импульса:  [9].

Отмечается полное отсутствие боковых лепестков, что обусловлено прямоугольным спектром частотной компоненты. Отметим, что сужение полосы частот прямоугольного спектра парциальных частотных компонент приводит к пропорциональному ухудшению разрешающей способности по скорости, а увеличение числа частотных компонент в той же общей полосе частот, занимаемой спектром ММЧ сигнала, позволяет увеличить интервал однозначности по задержке. При этом форма двумерных сечений в координатах «задержка-скорость» изменяется как качественно, так и количественно аналогично изменениям при ММЧ сигнале с прямоугольной огибающей импульса.

Выводы

1. Одним из перспективных направлений развития активной локации является синтез сложных широкополосных гидроакустических сигналов, основанный на спектральном представлении.
2. Энергетические спектры можно разделить на три класса: дискретный, полосовой и непрерывный.
3. Разбиение сигналов на классы эквивалентности в зависимости от групп преобразований (классификация сигналов), обусловлено необходимостью изменения структуры многочастотных по определенному принципу кодирования, применяя принцип дуальности временного и спектрального представления сигналов.
4. Синтез СШС в спектральной области позволяет получить достаточно эффективный метод получения гидроакустических сигналов с достаточно хорошими свойствами при решении задачи обнаружения.
5. Применение СШС с М-последовательностью в частотной области, позволяет получить ФН "кнопочного" вида, характеристики которой будут улучшаться с увеличением частотных компонент.
6.  При использовании СШП гидроакустического сигнала, необходимо учитывать, что спектр не только сдвигается, но и растягивается (сжимается).

Получены аналитические выражения для ФН для полигармонических и полосовых сигналов с учетом более точного учета эффекта Доплера и рассмотрены их свойства.

1. Вакман Д.Е., Седлецкий Р.М. Вопросы синтеза радиолокационных сигналов. - М.: Советское радио, 1973. - С. 243-244.

2. Варакин Л.Е. Теория сложных сигналов. - М.: Советское радио, 1970.

3. Варакин Л.Е. Системы связи с шумоподобными сигналами. - М.: Радио и связь, 1985. - 384 с.

4. Бутырский Е.Ю. Функция неопределенности сигналов на группе реобразований // Информация и космос. - 2008. - № 3. - С. 31-39.

5. Бутырский Е.Ю. Шклярук О.Н., Васильев В.В., Рахуба В.П. Способ обнаружения полигармонического сигнала. Патент на изобретение RU 2690317 C1, 31.05.2019. Заявка № 2018104720 от 07.02.2018.

6. Бутырский Е.Ю., Рахуба В.П. Полигармонические сигналы и их свойства // Национальная безопасность и стратегическое планирование. - 2020. - № 3(31) - . С. 37-50.

7. Бутырский Е.Ю. Функция неопределенности сигналов на группе преобразований // Информация и космос. - 2008. - № 3. - С. 31-39.

8. Бутырский Е.Ю. Математические модели гидроакустических сигналов и методы их обработки. - СПб: Стратегия будущего, 2018. - с. 613.

9. Бутырский Е.Ю. Взвешенное преобразование Гильберта. // Информация и космос. - 2008. - № 2. - С. 40-46.

10. Чапурский В.В. Избранные задачи теории сверхширокополосных радиолокаци-онньrх систем / В.В. Чапурский. - 3-е изд., испр. - М.: Издательство МГТУ им. Н. Э. Бау-мана, 2017. - 279 с.