Russian Federation
The new equations, due to the completeness of the accounting of natural and anthropogenic "loads" on the water environment, significantly increase the predictability of hazards: technical safety – in the form of estimates of the height of defence structures against floods of natural and anthropogenic origin; Safety of technical and organizational systems – in the form of assessments of consequences of unauthorized discharges of water bodies of accumulators in regulated runoff of watercourses and water bodies; Safety of navigation – in the form of calculations of water level surfaces in zones of limited depth of ship 's passage; Risks from emergency man-made and man-made disasters of hazardous pollutants; As well as allocation of recreational areas of water bodies and watercourses for sanitary safety. All hazard assessments can be performed in a "model foresight" diagnosis-prognosis system. I.e. Perform calculations of fluid dynamics in "space of specified hazards" using numerical simulation on equations obtained by the author and corresponding edge conditions. It is proposed to infer new equations of motion of viscous uncompressible liquid for watercourses, based on the Navier-Stokes equations in hydrostatic and Bussinesque approximations. A cosine projector of gravitational potential, "unfairly omitted" in the formalization of fluid motion since Leonard Euler and Daniel Bernoulli, has been introduced into the hydrostatic approximation. Two-dimensional motion equations (X, Y, t) for watercourses use an "unusual coordinate system": the action of the main force that causes the movement of the liquid in the watercourse, the acceleration of gravity, is "addressed" to only one axis of coordinates 0X. In the axis motion equation 0Y, the watercourse "becomes a body of water." Note that such a coordinate system is applicable for the movement of liquid under the action of gravitational potential only for its movement in the channel, pipe, channel - in the watercourse. Equations of motion are "closed in density," because they contain density of water and its gradients in the right part, and equations of turbulent diffusion of active impurities carry out transfer of density components. Differential operators of equations of different spatial dimension (X, Y, t), (X, t) have the same, universal form, which easily allows to formalize interaction of water bodies and watercourses in the dynamic system "river, watercourse - connected water body." The proposed viscous fluid motion equations are the ultimate generalization of "fine water" in spatial dimensions (X, Y, t), (X, t). The path of generalization summarization to the private representation of motion – to the "Bernoulli integral" is shown.
technogenic safety, safety of technical and organizational systems, safety of navigation, hydrographic network, equations, regional conditions, long waves, hydrology, hydraulics
Введение
Полным образом естественной макро гидрографической сети может служить Франция: приальпийские пруды-накопители, водосливы, ирригационные и судоходные каналы и реки, водохранилища, заливы, моря. В гидродинамической формализации и моделировании такой сети естественно использовать гидромеханические интерпретации модели «мелкой воды» в пространственно и динамически сложных композициях водотоков и водоёмов.
При выводе модифицированных уравнений «мелкой воды» временно-пространственной размерности использовалась простейшая форма автомодельности – постоянство всех суммируемых по вертикали функций. Это позволило сохранить в двумерном представлении уравнений движения вязкой жидкости нелинейные члены от трёхмерного Навье-Стокса и, разумеется, плоский лапласиан турбулентного обмена количеством движения. Это «сохранение» позволяет поставить на свободных жидких границах области решения краевой задачи математической физики краевые условия нового типа, а также сохранить механизм «свободной затопленной струи» от входящих источников количества движения.
Содержательно новым элементом новых уравнений движения является их «замыкание по плотности», полученное от использования известного гидростатического приближения движения жидкости по вертикальной координате. Таким образом, формально «локальный» прежде «динамический метод океанологии» (Н. Зубов, 1938 – аналог геострофической модели атмосферы, В. Бьеркнес, 1904) стал корректной частью общего формализма – двумерных уравнений («мелкой воды») движения вязкой несжимаемой жидкости. Сама же плотность, представленная в уравнении состояния солёностью воды и температурой, может уравнением турбулентной диффузии примесей «покомпонентно» считаться как пассивная примесь. Далее, уравнение состояния (в нашем случае – О. Мамаева) в каждой точке области решения краевой задачи по температуре и солёности формирует матрицу плотности воды и её значения передаются в уравнения движения.
Моделирование на сетке Карского моря показало, что пространственные градиенты плотности в 27 промилле (27 г хлор-ионов на 1л дистиллированной воды) создают перекос уровенной поверхности в зоне сопряжения с Обской губой в 80 см. Считалась «бароклинная» – замкнутая по плотности задача «по начальным данным» – полю солёности, как «действующей силы» ( полученной из средневзвешенных значений солёности воды по-вертикали) до стационирования численного решения краевой задачи. Для сравнения: такой же перекос уровенной поверхности создаёт действие ветра «силою» 10 м/с при решении баротропного варианта движения.
В работах автора, по-видимому, впервые в практике моделирования движения вязкой жидкости был предложен новый тип краевых условий – динамически адаптивный. Условия этого типа позволяют согласовывать вид краевого условия для одной функции уравнений краевой задачи с поведением решения на границе области решения другой функции.
Применение таких краевых условий существенно сокращает время стационирования численного решения краевой задачи: (20 -30)% на сетках Карского моря и Обской губы.
Представлялось желательным получить формализм, позволяющий моделировать естественную природную динамическую систему «река – присоединённый водоём» в понятной и единой математической и механической идеологии, в произвольной композиции их пространственных представлений и
.
1. Новые уравнения наклоненного движения размерности
1.1. Исходные уравнения
В качестве исходных уравнений для формализации наклонённого движения вязкой, несжимаемой жидкости – водотока возьмём уравнения Навье-Стокса в Буссинеска и гидростатическом приближениях.
Уравнения движения в сокращённой записи будут иметь вид:
=
,
=
(1)
=
,
=
 (2)
(2)
0= ,
=
(3)
Уравнение неразрывности:
, (4)
где, например,
Здесь все условные обозначения стандартные: – дифференциальные уравнения движения по координатным осям и
соответственно
– их «левые части»;
– составляющие скорости движения жидкости по осям координат
,
и
;
– символ дифференциального оператора;
– правые части уравнений движения; нижние индексы {
} – проекции на соответствующие оси декартовых координат;
– плотность воды;
– давление;
– текущие координаты соответствующих осей координат;
– время;
– коэффициент обмена количеством движения турбулентной энергии жидкости;
- вектор ускорения силы тяжести;
– единичные расходы воды, заданные в области решения и на контуре водотока;
– проекторы гравитационного потенциала на координатные оси
и
соответственно, заданные на всём пространстве решения краевой задачи;
– оператор Лапласа;
– углы наклона уровенной поверхности (назовём её для определённости «нулевой поверхностью») в проекции на координатные оси
и
, образовавшиеся от установившегося движения по заданным «расходам» водотока; расход – объём воды, проходящий через поперечное сечение водотока в единицу времени.
Угол
– угол наклона уровенной поверхности по оси
, адресованный только элементам дуг извилистого русла водотока и, тем самым, слагаемое
задано локально – в местах дугообразно искривлённого русла водотока.
Идея возможного учёта локального энергетического эффекта «дуг русла» принадлежит завлабораторией матмоделирования ГГИ, к.г.н., в.н.с., Маркову Михаилу Леонидовичу. Автор настоящей статьи его лишь оформил «в терминах уравнения».
Мы знакомы с этим эффектом, как рукотворным «гасителем центробежной силы» на крутых поворотах шоссе: поверхность дороги имеет наклон, направленный в сторону центра круга поворотной дуги. В водотоке гравитационный потенциал действует «локально» – на пространстве дуги поворота русла реки и выражается он углом наклона уровенной поверхности водотока направленной в сторону “угла падения» (14), знак угла падения определяется выбором направления оси 0Y.
Такая форма записей уравнений (1)–(3) сделана намеренно: в дальнейшем именно «правые части» уравнений движения будут главными объектами нашего внимания.
На рис.1 представлено схематически взаимодействие статических и динамических компонент наклоненного движения жидкости.
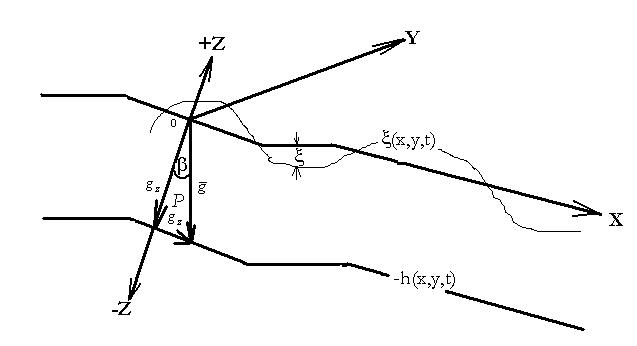
Рисунок 1 – Схема наклоненного движения
Здесь – след проекции уровенной поверхности на плоскости
,
– отметка дна – глубина водотока, отсчитываемая от дна до нулевой уровенной поверхности установившегося движения (от заданного начальными данными) расхода (ов) водотока.
Плоскость координат расположена на водной поверхности установившегося (от заданного расхода) наклоненного движения – «нулевой поверхности». Горизонтальная составляющая силы гравитационного потенциала действует только в направлении оси
, она совпадает с направлением стрежневого потока водотока. Ноль оси
находится на динамически подвижной уровенной поверхности установившегося (от заданного по начальным данным расхода) движения – на нулевой поверхности. Высотная отметка уровенной поверхности
(x,y,t)
может иметь разные знаки; отрицательное направление оси
совпадает с положительным направлением действия гидростатического давления; отметка дна является переменной функцией
:
,
, где координата
сохраняется , если формализовать заносимость водотока.
Хорошо видно, что здесь система координат водотока легко трансформируется в систему координат водоёма и наоборот. Действительно, повернём систему координат (рис.1) относительно оси против часовой стрелки так, чтобы gz совпала с
, тогда
=0, cos
и
соответственно, и мы получили водоём. Разница в системе координат в одном параметре. В системе координат - в водоёме
, в водотоке начальными данными задаётся вектор-столбец углов наклона нулевой уровенной поверхности жидкости
, полученный из натурных измерений наклонов уровенной поверхности водотока от средних и экстремальных расходов водотока в установившемся режиме его движения. Аналогично задаётся и вектор-столбец угла наклона уровенной поверхности на элементах дуг сильно искривлённого русла водоёма
.
Отметим важное свойство выбранной системы координат для водотоков: в двумерном представлении: оно позволяет «извилистое» русло реки «генерелизовать как прямолинейное», выделив участки русла с «существенными дугообразными искривлениями русла», где динамика потоков центробежным эффектом создаёт перекос уровенной поверхности и, таким образом, силу от гравитационного потенциала, представленную в записи правой части по оси
в форме (2). Таким образом, численное моделирование движения в водотоке позволяет использовать прямоугольную матрицу минимальной ширины, равной максимальному поперечному сечению водотока. В прежнем варианте – уравнений Сен-Венана такой возможности не было: извилистое русло вписывалось в прямоугольную матрицу «полностью», либо оно разбивалось на фрагменты и они «склеивались» по решению численной модели движения жидкости в водотоке.
1.2. Вывод правой части уравнения (1)
Итак, все предпосылки для получения формального обобщения движения вязкой несжимаемой жидкости для водотока и водоёма или их объединения «река – присоединённый водоём» в единой описательной системе мы уже имеем. Осталось проделать лишь простые, но важные процедуры с «правыми частями» уравнений (3) и (1). Вывод для «левых частей» уравнений (1), (2), понижающий пространственную размерность до
, осуществляетя процедурой аналогичной для вывода правой части уравнения (1) и потому опущен.
Из уравнения (3) получаем с помощью интегрирования по вертикали выражение для давления жидкости
. Подставляем его в правую часть уравнения (1) и интегрируем почленно все дифференциальные операторы уравнеия (1) по вертикали
с гипотезой постоянства по
всех суммируемых функций. Суммирование по
осуществляется в пределах:
- верхний предел и –h – нижний предел. Заметим ещё раз, что поскольку процедура вывода сводится к дифференцированию интеграла по переменным пределам – стандартной процедуре, мы приводим вывод лишь для наиболее полной правой части уравнения (1).
Итак:
;
(6)
Т.о., (**)
- атмосферное давление (7)
, член с
в дальнейшем опустим (8)
Подставим (8) вместо P в (1) :
, (9)
Проинтегрируем правую часть (1) по z, подставив туда (9) :
=
, (10)
Интегрируем почленно квадратную скобку (10):
,
;
A: -
А: - ;
А: - ;
В: , собирая А и В, имеем:
g
cos
, (11)
1.3. Основные свойства
Анализируя полученное, можно легко видеть новые и содержательные результаты. Пожалуй, самый удивительный из них - это давление столба воды: в наклонённом движении оно в раз меньше «ненаклонённого».
- в водотоке и
- водоёме! Это хорошо видно и образно и формально: вращая относительно
рис.1 по часовой стрелке, мы приходим к свободному падению жидкости:
,
. Вращая против часовой стрелки, получим:
,
. Удивительно, что эту очевидность не заметил ни Леонард Эйлер, ни Даниил Бернулли, ни многочисленные их преемники!
Выражение (11) позволяет получить интересный качественный результат: первый член этого выражения обслуживает водоём и водоток, а второй – только водоток. При этом, наличие выражения показывает, что в каждой точке изменения градиента наклона нулевой уровенной поверхности (фактически угла наклона «подложки» водотока в направлении оси 0X) в зависимости от его знака производится ускорение (или) замедление скорости движения жидкости пропорциональное действию множителя градиента нулевой поверхности.
Ещё одно интересное свойство: групповая скорость длинных волн , тогда, положив в (11) для наглядности оценки
и, сгруппировав оставшиеся члены относительно
, получим:
, для сравнения в водоёме:
. Таким образом, можно производить оценки длинноволновой передачи количества движения в водотоке и водоёме по заданным
и рассчитанным
параметрам приведённого выражения.
Для получения «полной» правой части уравнений движения вязкой жидкости, где бы содержались все «массовые силы» следует добавить: ветер, трение о дно и (для больших водоёмов) эффект Кориолиса. Первые две часто вводят, используя некий элемент математического кокетства: ветер - ; трение о дно -
(как краевые условия при интегрировании по
уравнений (1), (2)), где
- заданные безразмерные константы, полученные из опыта;
,
определяется аналогично
;
задаются соответственно покомпонентно для уравнений (1) и (2);
задаются также покомпонентно. Для нас здесь важно то, что это производные от «обобщённой массовой силы» - давления
. На поверхности воды эта массовая сила «превращается» в ветер, у дна – в трение о дно. И, очевидно, эти массовые силы для водотока должны содержать множитель
. Представляется, что ветер и трение о дно с позиции «правой части» было бы правильнее трактовать как «энергетическую добавку-вычет» - ветер и «энергетический вычет» - трение о дно и формально представлять их чисто эвристически. Т.к., и то, и другое есть «внешнее для жидкости трение», т.е. самой жидкости не принадлежит и, в силу этого обстоятельства, не может быть (замкнутой) частью её (жидкости) формализма. Существенно здесь то, что «оба трения» заданы универсальной для механики жидкости и газа формой – «квадратической».
Таким образом, наиболее полное представление правой части уравнения (1) для потока можно записать в виде:
, (12)
Здесь – уклоняющая ( вправо, в северном полушарии и влево – в южном полушарии Земли) движение жидкости сила – эффект Кориолиса. Как упоминалось выше, этот эффект «не принадлежит» водотоку в уравнениях движения вязкой жидкости, он «принадлежит» большому водоёму, например, морю. Кориолис содержится в выражении (12) потому, что мы хотим использовать универсальное математическое представление для водотока и водоёма, т.к. намереваемся в дальнейшем формализовать динамическую природную систему «воток – присоединённый водоём». Например, «река – озеро; губа, море».
-
-
Уравнения:
-
(13)
(14)
(15)
(16)
, (17)
где:
– локального действия член, отнесённый к дугам поворота русла водотока,
– наклон уровенной поверхности направленный по оси
в сторону центра дуги поворота русла водотока. Здесь, как и в традиционной форме записи уравнений движения Сен-Венана, действие гравитационного потенциала в направлении оси
можно справедливо считать как «слабонаклонённое», ибо это соответствует натурным измерениям. Тогда компоненту давления в векторе сил гравитационного потенциала можно (в силу её малости) опустить, оставив для оси
только выражение
;
U,V (u;v)H; u,v – «эйлеровы скорости» размерности (x,y,z,t);
H , hi;j =
– заданная матрица глубин;
(
)H - заданные коэффициенты турбулентного обмена количеством движения и массой;
– заданный вектор-столбец углов наклона нулевой уровенной поверхности водотока;
– вектор ускорения силы тяжести;
– плотность воды; (17) – уравнеие состояния жидкости;
=2
,
- угловая скорость вращения Земли,
- географическая широта места;
–- касательное напряжение трения ветра о водную поверхность;
– эмпирический коэффициент;
c – коэффициент придонного трения;
, i = 1,2,3; c1
S – соленость;
– температура воды;
– пассивная примесь;
Здесь уместно привести сравнение «классического» уравнения «мелкой воды» (например, для переменной X), полученного из уравнений Навье-Стокса при помощи «теоремы о среднем значении функции», приведённого в работе [1] и нашего уравнения (13) – для водоёма:
– «мелкая вода» (МВ), (18)
Всё очевидно без комментариев, если сравнить МВ с уравнением (13). Гидродинамики «от гидрологии» и «гидравлики» для водотоков использовали одномерный (X,t) аналог уравнения (18) (с «вычёркиванием» Кориолиса и добавлением
, а также заменой
на Q
и
на
, где
– ширина водотока) – уравнение Сен-Венана. Применение этого уравнения для формализации движения воды в водотоках сопровождалось комментарием: «для небольших уклонов дна водотока».
Обращаем внимание на уравнение (14). Хорошо видно, что это уравнение движения вязкой жидкости «главным образом» для водоёма, а член нулевого порядка с наклоном уровенной поверхности по оси задан «локально». Это одно из самых сильных «завоеваний» предложенной модели водотока в данном
представлении. Система координат «положена» на нулевую уровенную поверхность и «автоматически» поворачивается вслед за направлением стрежневого потока – осью
.
В каких ситуациях двумерное моделирование динамики потоков и массопереноса в водотоках может быть целесообразным. В режимно-гидрологических прогнозах речной сети, имеющей крупные водотоки и притоки с большими наклонами нулевой уровенной поверхности: время прихода паводочной волны, расчёт площадей затоплений, расчёт времени вскрытия ледяного покрова от попуска большого расхода. В русловых процессах: заносимость каналов судового хода, эрозия берегов, формирование баров. В гидротехнике: расчёт потоков и массопереноса для проектирования на водотоке любых строительных конструкций. В водоснабжении: расчёты оптимальных размещений сбросов и водозаборов на разных берегах водотока – контроль и управление загрязнением. В санитарной гигиене: расчёты массопереносов для выделения рекреационных зон и оценок последствий техногенных катастроф. В безопасности судоходства: расчёт экстремалей уровенной поверхности от действий ветра, приливов и аварийных сбросов-попусков.
Можно заметить, что левые части уравнений (14) и (13) для водотока точно соответствуют математической модели «затопленной струи вязкой несжимаемой жидкости» и, таким образом, формально описывают «струйный эффект» от притоков-источников, заданных на контуре области решения краевой задачи.
Содержательно значимым качеством новых уравнений движения вязкой жидкости для водотоков является их «всенаклонённость», т.е. движение под действием гравитационного потенциала (уравнение (13)) определено на полуинтервале . При
– свободное падение жидкости. Наличие в уравнении (13) члена с градиентом угла наклона нулевой уровенной поверхности
позволяет каждой точке водотока, где происходит изменение угла
, быть локальным источником ускорения или замедления скорости движения жидкости в зависимости от знака градиента угла
.
Правой части уравнения (13), приведённой ниже, можно придать и такое качественное толкование членов, связанных с квадратной скобкой:
, как известно,
– групповая скорость длинных волн жидкости, тогда
можно интерпретировать как длинноволновой перенос совокупного аддитивного действия: градиента плотности, динамической уровенной поверхности, наклона нулевой уровенной поверхности и её градиента.
Сохранение в уравнениях движения (13), (14) «двумерного Лапласиана» вызвано не столько энергетическими или «струйно-имитационными соображениями», сколько постановочными. Плоский Лапласиан позволяет на жидких границах области решения задачи динамики и загрязнения потоков ставить условие второго рода – «протекание» и, таким образом, сохранять для численного решения на этих границах соответствующие нелинейные члены уравнений движения.
Обращаем внимание на интересный факт. Ниже будет показано как, не решая краевой задачи, можно из уравнения (13) получить расчёт параметров водослива, например, плотины гидроэлектростанции.
В предельном случае установившегося движения (от действия гравитационного потенциала) из уравнения (13) можно получить: , (*). Разрешая это выражение относительно c, получим:
. Хорошо видно, что выражение (*) превращается в тождество, если
, а
. Это достигается при «чисто» длинноволновом механизме передачи количества движения. Таким образом, мы достигли «локального» динамического минимума правой части уравнения (13). «Глобального» минимума правой части Fx можно достигнуть, если в выражении (11) «занулить» второй член, т.е. найти корни дифференциального выражения в круглых скобках:
. Это и есть «описатель» сопряжений наклонённой плоскости – плотины и двух горизонтальных плоскостей: верхней и нижней. Т.е. мы достигаем глобального минимума правой части уравнения движения (13) Fx для «всенеклонённого» движения в водотоке.
min достигается, если S=
Это компактное выражение для радиуса сопряжения горизонтальных и наклонной плоскостей
было получено доцентом факультета прикладной математики и процессов управления СПбГУ, к.ф.-м.н. Станиславом Константиновичем Мышковым. Здесь S
– длина дуги сопряжения поверхностей-плоскостей, имеющих различные (заданные начальными данными) углы наклона
, а
– радиус сопряжения водослива. Для плотин-водосливов: горизонтальной
и наклоненной
плоскостей дугой S
. Т.е. дуга сопряжения «угловой точки» «начинается» на горизонтальной плоскости (поверхности) с высотной отметки h (
) и «заканчивается» на наклонной плоскости с отметкой
, где
. Знак x определяется типом сопряжения поверхностей: «+» – вогнутый (для плотин-«носок»), «-» - выпуклый (для плотин-«конек»).
2. Одномерное представление движения под действием гравитационного потенциала
Вывод одномерных уравнений движения и неразрывности, а также турбулентной диффузии примесей осуществляется процедурой «интегрирования» соответствующих двумерных уравнений по мере
c гипотезой постоянства по ней всех суммируемых функций. Таким образом,
=
, также равны нулю и соответствующие дифференциальные операторы по
в уравнении неразрывности и турбулентной диффузии примесей.
Покажем процедуру суммирования по правой части уравнения (13) на ее первом члене (суммирование проводим по ширине водоема-водотока от 0 до B(
)):
Таким образом, одномерный аналог «правой части» двумерного представления безнапорного движения вязкой несжимаемой жидкости (9) будет иметь вид:
,
Вид одномерного уравнения движения вязкой жидкостис с точностью до обозначений совпадает с двумерным:
, (19)
где Q – расход воды водотока,
- площадь поперечного сечения водотока ,
– ширина водотока.
Будем использовать уравнение (19) – предельное по полноте представление уравнение движения вязкой жидкости типа Навье-Стокса в одномерном представлении в гидростатическом приближении исходных примитивных уравнений.
«Идя в направлении поиска Бернулли», упростим его, сохранив представление вида:
(20),
Поскольку Бернулли получил своё соотношение для трубы, её «сечения», то «уберём» свободный уровень и соответственно
, заменим на
.
Положим также угол наклона уровенной поверхности водотока установившегося движения или угол наклона продольной оси трубы .
Далее вводим известные соотношения:
,
– площадь поперечного сечения трубы (водотока), (К)
Итак, мы имеем уравнение:
(21)
Используя соотношения (К), запишем:
Далее используя: , получим:
.
Полагая (для сечения трубы) , получим
, (22)
где .
Здесь атмосферное давление опущено, поскольку опущено и в «исходном» уравнении (19).
Выражение в круглых скобках (22) и есть «сохранение Бернулли». Вывод «сохранения Бернулли» опубликован в работе [5]. Здесь важно, однако, напомнить, что (22) получено при предположении, что ( ,
)
,
, а также для скорости движения вязкой несжимаемой жидкости использована «групповая скорость длинной волны», что естественно для диапазона применимости уравнения общего вида: «труба – река – губа – море». Бернулли также оговаривает «горизонтальность» трубы.
О краевых условиях «адаптивного» типа на свободной жидкой границе области решения краевой задачи.
Для уравнений турбулентной диффузии примесей:
, (23)
Для уравнений движения:
Г
=
, (24)
Условия (23), (24) поставлены сообразно поведению решения на жидкой границе нормальной компоненты потока : если жидкая граница является «стоком» потока (направление внешней нормали) – условие втрого рода («протекание»), если же граница является «источником» (направление внутренней нормали) – «алгоритмическое» условие первого рода: сохраняется значение функции предыдущего временного слоя численного решения краевой задачи.
Понятно, что эти условия могут действовать «по-разному» в каждой точке жидкой границы. Условие (24) формализует одновременный расчёт действия сгона-нагона и прилива-отлива как в водоёме, так и в водотоке. У нас такой динамикой потоков обладает Северная Двина.
Условные обозначения стандартные. – заданные на жидкой границе амплитуды
и фазы
приливного потока.
Об адаптивности краевых условий на свободной жидкой границе. Сравнивалось время стационирования решения краевой задачи (13) – (17); (23), (24); с условиями первого рода для источников области решения и стандартными начальными условиями: нулевыми значениями компонентов потоков скорости жидкости внутри области решения вплоть до свободной жидкой границы области решения и начальное распределение (в узлах сетки области решения) только солёности, и вариант с постановкой краевого условия на свободной жидкой границе «стандартного» вида - второго рода (сток). Второй (не адаптивный) вариант вида краевых условий численного решения краевой задачи на сетках Обской губы и Карского моря стационировал решение указанной задачи на 25% дольше.
В заключение можно рекомендовать «различительно-наглядную» запись пространства предложенных уравнений: и
. Она позволяет с помощью «добавки z» различить вариант записи уравнений для водоёма и водотока со «свободной уровенной поверхностью жидкости – малой z» от «несвободной»: трубы, подлёдного движения в водотоке или водоёме:
и
.
Прикладные задачи-модели вязкой несжимаемой жидкости класса «мелкая вода» для гидрографических сетей в начале своего пути. Временно пространственная комбинаторика численного моделирования водоёмов и водотоков сети может быть большой, тогда такая форма записи «пространства» уравнений передаст «различение» компьютерам и сократит энергию поиска нужного варианта.
Заключение
Предложена универсальная форма записи уравнений движения вязкой жидкости в рамках модельного приближения «мелкой воды», временно-пространственной размерности для водоёмов, водотоков, плотин-водостоков и каналов. Она позволяет легко формализовать макро гидрографическую сеть, представленную различными композициями природных и антропогенных водотоков и водоёмов любых масштабов.
В заключение можно сформулировать концептуального класса обобщения:
-
в научной литературе для уравнений математической физики часто безответственно используется категория «сохранение»: мы, как правило, имеем дело с «открытыми динамическими системами», а тогда при постановке краевой задачи математической физики необходимо в области решения и не её границах задать соответствующие «стоки» и «источники», ибо никакого «сохранения автоматически» в природе нет;
-
третий закон Ньютона (о «действии и противодействии»), необоснованно интерпретируемый, как «бесконечно действие», в предложенном обобщении «мелкой воды», имеет конечную скорость действия аддитивно заданного «носителя силы», и она равна групповой скорости длинной волны;
географические гидрология суши, океанология и инженерная гидравлика обрели свои «академические основания» в гидродинамике «мелкой воды», позволяющие просто и доходчиво сформировать понятийно предметную базу у проектантов, студентов и аспирантов.
1. Molchanov V.N. Gidrodinamicheskaya model' cirkulyacii v vodoeme proizvol'noy formy s proizvol'nym naborom zagryaznyayuschih istochnikov, imeyuschih diffuzionnyy harakter // Materialy Vsesoyuznogo simpoziuma «Okeanograficheskie aspekty ohrany vod ot himicheskih zagryazneniy». - M.: AN SSSR, 1975. - S.88-93.
2. Molchanov V.N. Novye uravneniya naklonennogo dvizheniya vyazkoy zhidkosti razmernosti (X,Y,t) i (X,t), postanovki kraevyh zadach // Sbornik trudov III Mezhdunarodnoy konferencii «Estestvennye i antropogennye aerozoli» 24-27 sentyabrya 2001. - SPb, 2001. - S. 519-528.
3. Molchanov V.N. Dvumernye modeli dinamiki potokov i zagryazneniya ust'evyh vzmor'ev: avtoref. diss. na soiskanie uch. st. k.f.-m.n.: FM № 008411, AANII. - L.,1979. -17 s.
4. Molchanov V.N. «Trilogiya». - SPb: Strategiya buduschego, 2011. - 229 s.
5. Molchanov V.N. Modelirovanie makro gidrograficheskih setey, kak dinamicheski otkrytyh vodnyh sistem: kraevye usloviya «stok», «istochnik» // Materialy X Mezhdunarodnoy konferencii «Estestvennye i antropogennye aerozoli», Sankt-Peterburg 21-25 maya 2016. - SPb: Izd-vo VVM, 2016 - S. 66-78.






